CTF Crypto Challenge Writeup: Cracking the Hatmash Hash Function with Matrix Operations

• Challenge: hatmash
• Category: crypto
• Solution: solve.py

Challenge

What do you mean “We think you spend too much time with matrices.”? It’s just a hash function, jeez…

Explore and Analysis

hatmash.py is the only file released to the competitors. After read through the functions and some verification, we can easily tell it’s all about matrix operations defined on logical matrices, or 0-1 matrix in some context. Our goal is to find a collision.

To begin with, we read through the helper functions.

def bytes_to_mat(x):
    assert len(x) == 32
    bits = list('{:0256b}'.format(int.from_bytes(x, 'big')))
    return [[int(j) for j in bits[i:i + 16]] for i in range(0, 256, 16)]


def mat_to_bytes(x):
    return int(''.join([str(i) for j in x for i in j]), 2).to_bytes(
        (len(x) * len(x[0]) + 7) // 8, 'big')


def mod_mult(a, b, m):
    assert len(a[0]) == len(b)
    return [[sum([a[k][i] * b[i][j] for i in range(len(b))]) % m for j in
             range(len(a))] for k in range(len(a))]


def mod_add(a, b, m):
    assert len(a[0]) == len(b[0]) and len(a) == len(b)
    return [[(a[i][j] + b[i][j]) % m for j in range(len(a[0]))] for i in
            range(len(a))]

• bytes_to_mat() converts the passed in bytes string to its binary representation in 256 bits and make a 16*16 logical matrix.
• mat_to_bytes() just reverse the above process
• mod_mul(a, b, m) is equivalent to the following numpy statement return (a @ b) % m, where @ is the matrix multiplication operator.
• mod_add(a, b, m), similarly, return (a + b) % m

def mash(x):
    bits = list('{:0{n}b}'.format(int.from_bytes(x, 'big'), n=8 * len(x)))
    if bits.pop(0) == '0':
        ret = A
    else:
        ret = B
    for bit in bits:
        if bit == '0':
            ret = mod_mult(ret, A, 2)
        else:
            ret = mod_mult(ret, B, 2)
    lenC = C
    for _ in range(len(x)):
        lenC = mod_mult(lenC, C, 2)
    return mat_to_bytes(mod_add(ret, lenC, 2))

Except helper functions, mash(x) is the only interesting function here. A bytes string with length n is converted to its binary representation, this should be the passphrase we want to generate.

For each bit in its binary representation, based on the bit value, A or B is matrix multiplied to the right. Then C^(n+1) is added to the result. Equivalently,

T = {A, B}^n + C^(n+1), where A, B, C, T are logical matrices

So our goal to the challenge is to find a passphrase other than gib m3 flag plox? and make a collision, mash(passphrase) == mash(b'gib m3 flag plox?').

Approach to the solution

The first thing I did was to write everything in numpy. numpy array is implemented based on C/C++ and use multiprocessing for matrix multiplication which greatly increase the runtime speed.

Then I implement a DFS and a random search algorithm to brute-force a passphrase. Unfortunately, it’s not that easy.

Then I try to work on the properties of random generalized square matrix and logical matrix. I noticed that almost every random initialized 16*16 logical matrix is invertible (with ~ (16*15/2) / 2^16 ~= 0.35%it’s not). And elementwiseA + B = A xor B, A \* B = A & B for A, B logical matrix. But they didn’t extend to matrix multiplication. I also thought of matrix decomposition, but didn’t make more progress in the end.

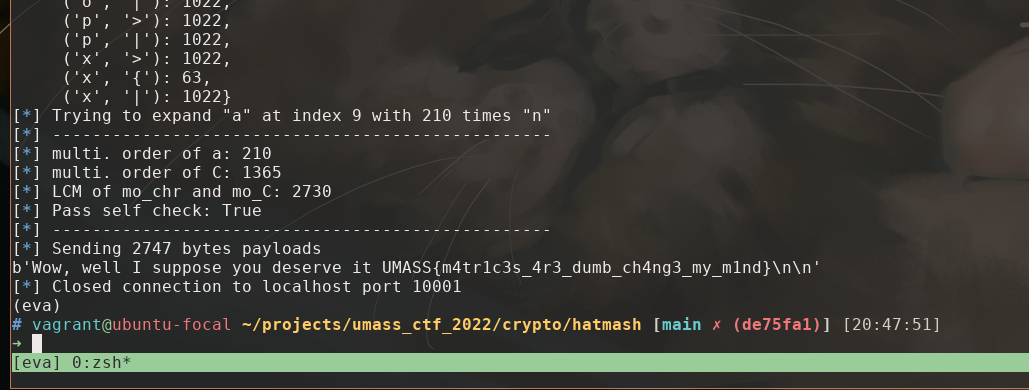
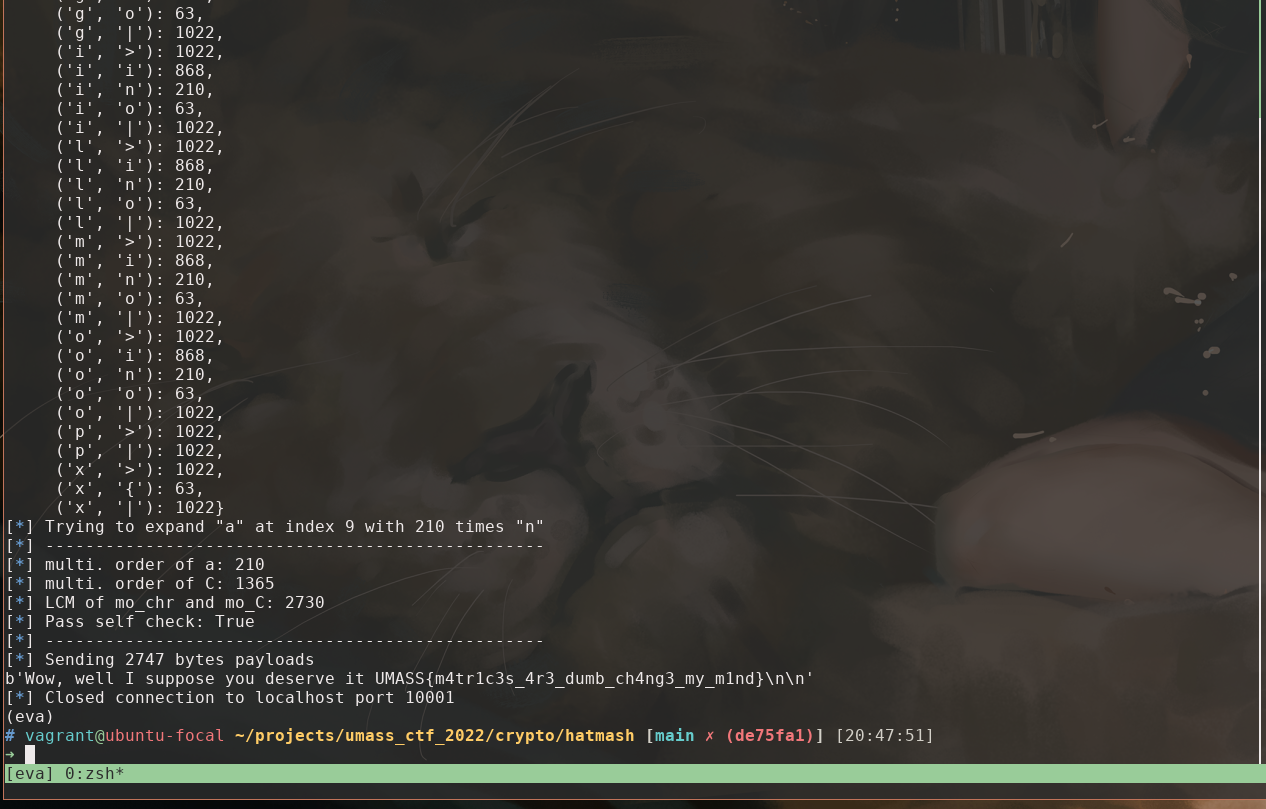
Finally, I turn in to multiplication order or logical matrices. That is for logical matrix A, if A^i = A, then i-1 is the multiplicative order of A defined for this group. If we can find one letter from the actual passphrase gib m3 flag plox? whose matrix representation after mash(c) is small, we expend it s.t. ccccccccc...ccc and c gives the same result after the sequence of A and B multiplication, and somehow it doesn’t change C^(n-1) , we made a collision.

So my algorithm is

1. compute multi. order for all letters in gib m3 flag plox?, find the one with least mult. oder, donote it c, and denote its multi. order m.
2. compute multi. order for C, denoted n
3. calculate the least common multiple of m and n, lcm(m, n)
4. insert lcm(m, n) times c before its occurrence in the passphrase
5. restart the process if the multi. order of any necessary matrix is too large for a payload.

Implemented at solve.old.py.

Shorter payload

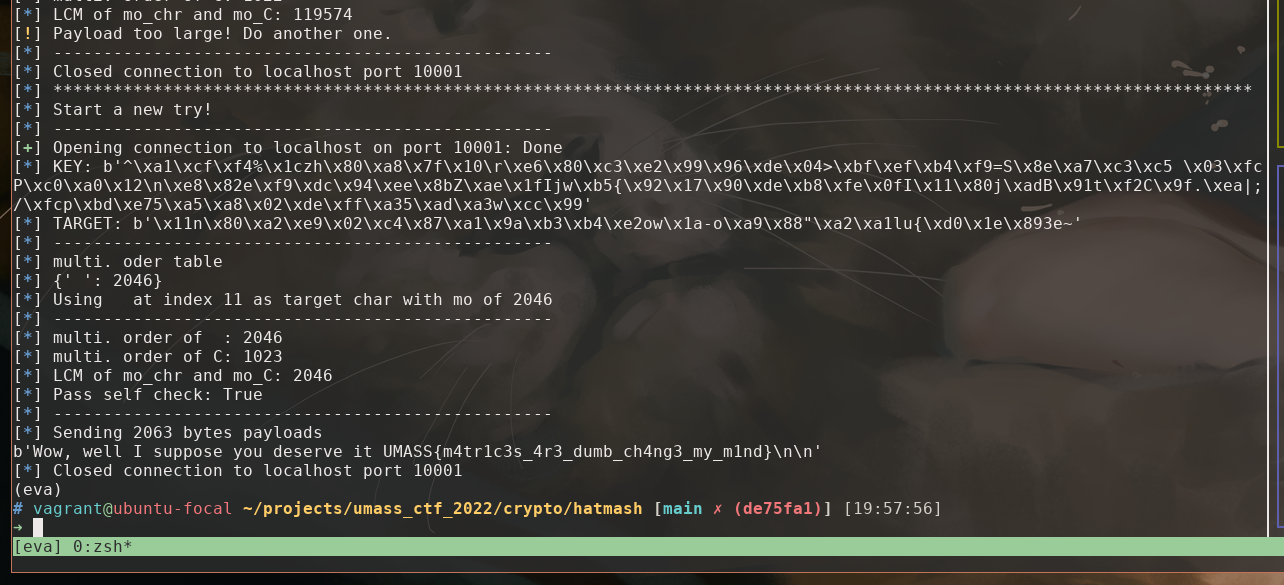
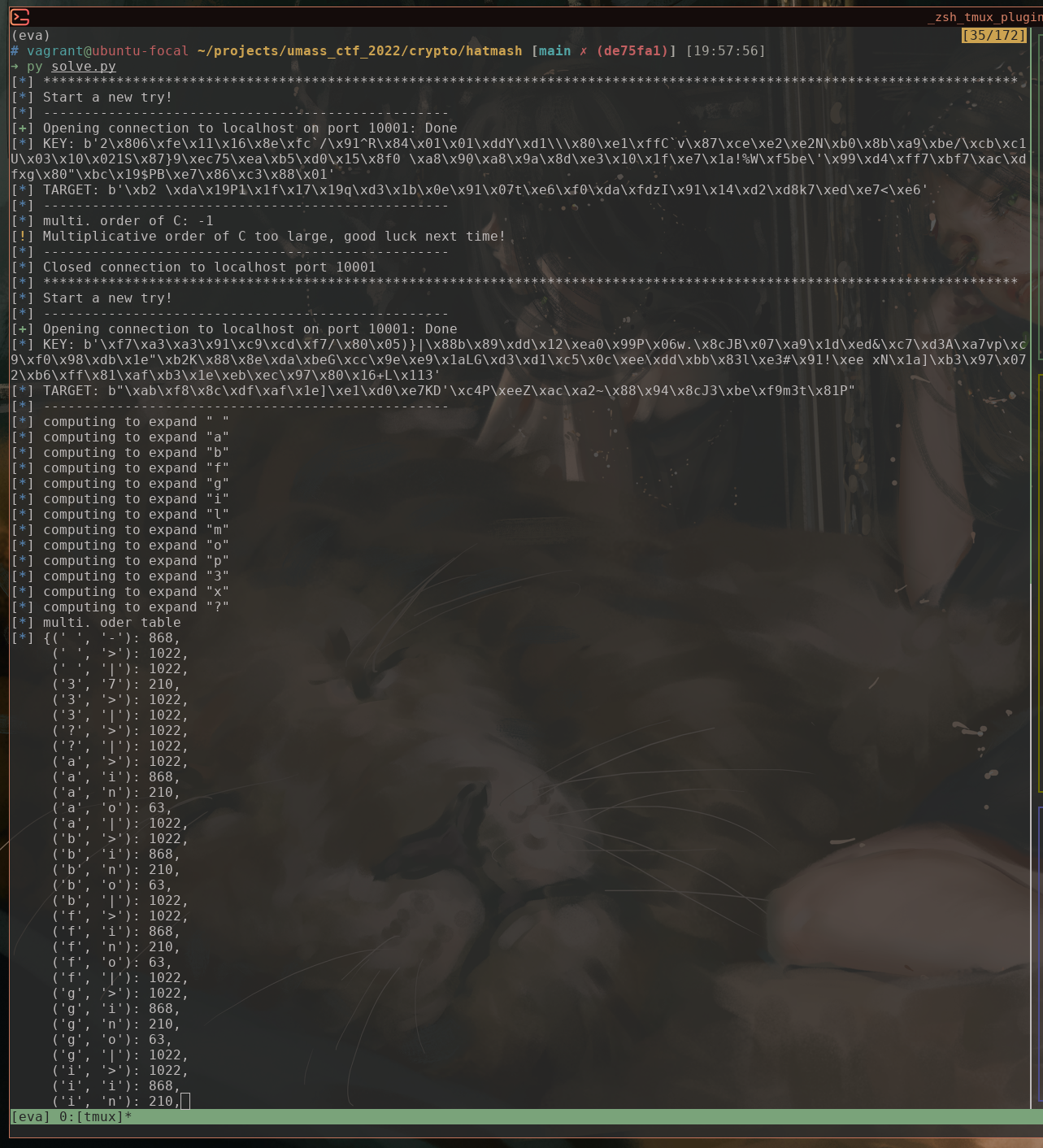
numpy matrix multiplication is fast, so we don’t care much in computing the multi. order. But we don’t want payload to be too large b/c hatmash.py implemented naive matrix multiplication and that is thousands of times slower.

An improvement would be using aaaaaaa...aaab to expand b instead of just bbbbbbb...bbb. This allows us to potentially use any character in the ALP.

So we compute all possible combination to expand t with cccc...ccct, and choose the one that has least lcm(m, n).